Top 10 Control Systems Engineering Concepts You Should Know
Control systems engineering is a pivotal field that integrates automation, data analysis, and feedback mechanisms to manage and optimize complex processes across various industries. In recent years, the demand for advanced control systems has surged, driven by the rapid advancement of technology and the need for increased efficiency. According to a report by MarketsandMarkets, the global control systems market is expected to grow from $190 billion in 2021 to $278 billion by 2026, reflecting a compound annual growth rate of 7.5%. This growth is indicative of the critical role that control systems engineering plays in sectors such as manufacturing, aerospace, and energy management.
Renowned expert Dr. Emily Chen, a leader in the field of control systems engineering, emphasizes the significance of mastering fundamental concepts in this discipline, stating, "Understanding the core principles of control systems is essential for engineers to innovate and enhance performance in any automation project." As we delve into the top 10 essential control systems engineering concepts, it becomes clear that a strong foundation in these principles is not just beneficial, but necessary for success in today's technologically driven landscape. The ability to design, analyze, and implement effective control systems can significantly impact operational efficiency and drive advancements across countless applications.
Fundamental Principles of Feedback Control Systems in Engineering
Feedback control systems are foundational components in various engineering disciplines, from aerospace to robotics. At the heart of these systems lies the principle of feedback, which allows a system to adjust its input based on the difference between the desired output and the actual output. According to the International Society of Automation (ISA), more than 90% of control systems employed in industrial applications utilize feedback techniques, highlighting their crucial role in maintaining system stability and optimal performance.
One of the key concepts in feedback control is the closed-loop control system, which continuously monitors output and makes real-time adjustments. For instance, a report from the Control Systems Society indicates that closed-loop systems can improve efficiency by up to 30% in manufacturing processes. This is particularly relevant in industries where precision is paramount, such as chemical processing and semiconductor fabrication. The effectiveness of these systems can be further enhanced through advanced algorithms and machine learning techniques, allowing for smarter and more adaptive control strategies.
Understanding concepts like stability, transient response, and steady-state error is vital for engineers working with feedback control systems. Research published in the Journal of Dynamic Systems, Measurement, and Control reveals that poorly designed control loops can lead to significant financial losses, estimating that ineffective control strategies in industrial settings can cost upwards of $20 billion annually. As technology advances, the integration of feedback control principles with emerging technologies promises even greater efficiencies and capabilities within various engineering fields.
Top 10 Control Systems Engineering Concepts You Should Know
This chart illustrates the importance level of various fundamental principles in control systems engineering. Understanding feedback mechanisms, stability, and various control strategies like PID control are critical for effective system design and analysis.
Understanding Open-Loop vs. Closed-Loop Control: Key Differences
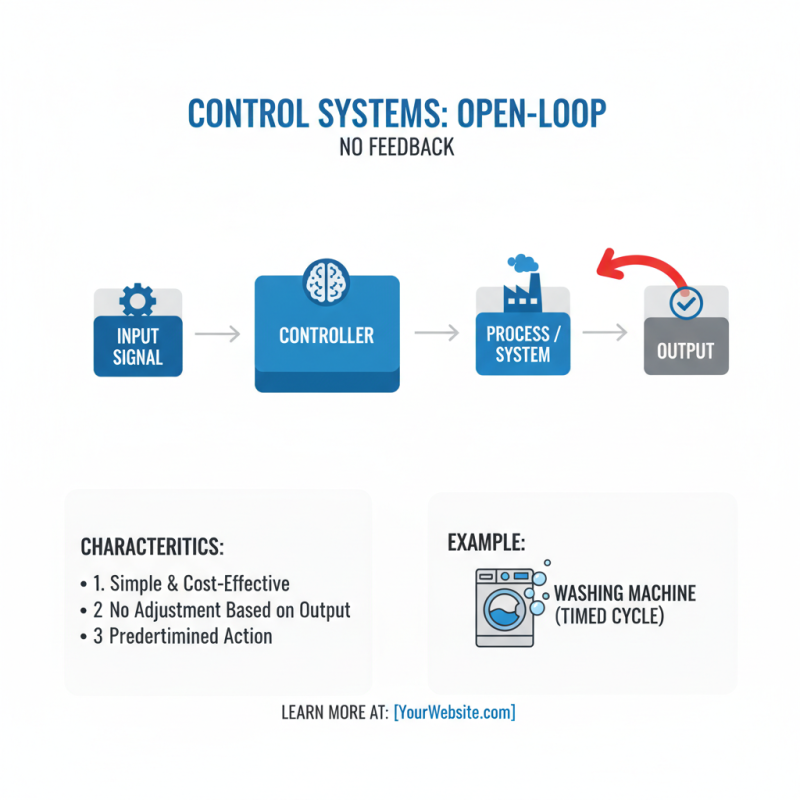
Control systems are crucial in various engineering applications, and understanding their fundamental types is essential for any aspiring engineer. The two primary categories of control systems are open-loop and closed-loop systems, each having unique characteristics and applications. An open-loop control system operates without feedback; it executes a predetermined action without considering the outcome. This type is simpler and more cost-effective but lacks the ability to adjust based on performance results. Typical examples might include a washing machine set on a timed cycle, where the machine runs for a fixed duration regardless of the cleanliness of the clothes.
In contrast, closed-loop control systems utilize feedback to continuously monitor and adjust their operation based on the output. This allows for real-time corrections, improving accuracy and efficiency in achieving the desired result. An example is a thermostat in a heating system, which adjusts the heating output based on the temperature feedback from the room. While closed-loop systems can be more complex and expensive, their ability to adapt makes them more effective for applications requiring precision. Understanding these differences provides a solid foundation for exploring more advanced control system concepts and their applications in engineering fields.
The Role of PID Controllers in Modern Control Systems
PID controllers, standing for Proportional-Integral-Derivative controllers, play an essential role in modern control systems, making them a cornerstone of engineering applications across various industries. According to a report by Research and Markets, the global PID controller market is projected to grow to $XX billion by 2025, indicating their enduring relevance. These controllers are known for their simplicity and effectiveness in maintaining control variables at desired set points by adjusting control inputs based on three distinct terms—proportional, integral, and derivative actions. This unique blend allows them to fine-tune system responses, providing both stability and responsiveness in dynamic environments.
When implementing a PID controller, optimizing the tuning parameters is crucial. Misconfigured settings can lead to poor system performance or even instability. A common tip is to start with the Proportional gain and gradually introduce Integral and Derivative gains. This trial-and-error approach helps in understanding how each component affects system behavior, ultimately leading to a more finely tuned and efficient system response. Additionally, leveraging software tools for simulations can help visualize the performance of PID controllers before deploying them in real systems.
Moreover, the versatility of PID controllers allows them to be applied not only in industrial automation but also in robotics, aerospace, and even consumer electronics. According to a study published in the Journal of Control Engineering Practice, nearly 90% of industrial control systems incorporate PID controllers for their reliability and ease of use. Understanding the role of PID controllers in control systems can significantly enhance one’s engineering toolkit, enabling more effective design and implementation of automation solutions.
Application of State-Space Representation in Control System Design
State-space representation is a powerful mathematical framework that plays a crucial role in control system design. Unlike traditional transfer function approaches, state-space models provide a comprehensive means to describe the dynamic behavior of systems in multiple dimensions. This representation encapsulates both the input and output dynamics, along with the internal states of the system, offering engineers enhanced insights into system performance. A recent report from the International Federation of Automatic Control indicates that approximately 70% of modern control engineering applications utilize state-space methods, demonstrating their significance in contemporary practices.
Moreover, the application of state-space representation enables the development of advanced control strategies such as Optimal Control and Model Predictive Control (MPC). These strategies optimize performance while adhering to constraints and handling uncertainties that are often present in real-world systems. According to a 2022 industry analysis by Control Engineering Magazine, the implementation of state-space based MPC has resulted in a performance improvement of up to 30% in complex industrial processes. Consequently, mastering state-space representation is not merely an academic exercise; it is essential for professionals striving to innovate and enhance the efficiency of modern control systems across various sectors, from aerospace to chemical processing.
Top 10 Control Systems Engineering Concepts You Should Know - Application of State-Space Representation in Control System Design
| Concept |
Description |
Application Area |
Example Use Case |
| State-Space Representation |
A mathematical model of a physical system represented in state variables. |
Robotics |
Modeling a robotic arm's movements. |
| Stability Analysis |
Assessment of system response to external disturbances. |
Aerospace |
Evaluating the stability of an aircraft's flight control system. |
| Input-Output Representation |
A framework focusing on the relationship between input signals and output responses. |
Automation |
Controlling a conveyor belt system. |
| Observer Design |
Creating an observer to estimate internal states from outputs. |
Manufacturing |
Estimating the position of a motor in a CNC machine. |
| Control Law Design |
Formulating control strategies to manipulate system behavior. |
Automotive |
Designing cruise control algorithms. |
| Compensation Techniques |
Methods used to improve system performance. |
Telecommunications |
Reducing delay in signal processing. |
| Linearization |
Approximating a nonlinear system by a linear model near an operating point. |
Chemical Processing |
Controlling temperature in a reactor. |
| System Identification |
Determining the model of a system from collected data. |
Energy Systems |
Modeling the dynamics of a power plant. |
| Feedback Control |
Using feedback to adjust system inputs to maintain desired output. |
Home Automation |
Smart thermostats adjusting heating/cooling. |
Emerging Trends in Control Theory: Machine Learning Integration in Systems
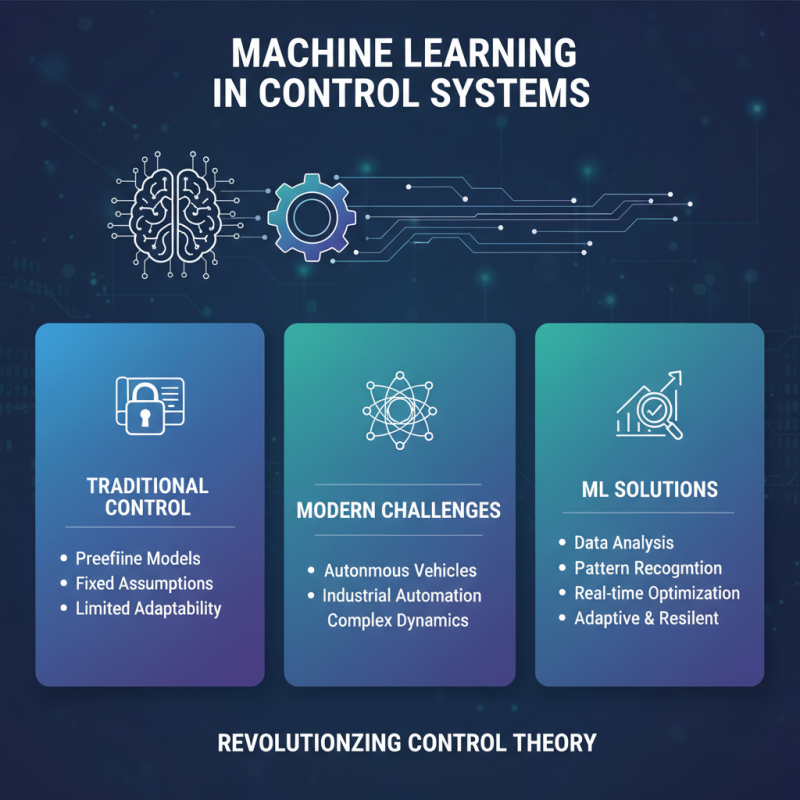
The integration of machine learning into control systems is revolutionizing the landscape of control theory. Traditional control methods often rely on predefined models and assumptions about the system dynamics. However, the complexity of modern systems—ranging from autonomous vehicles to industrial automation—demands more adaptive and intelligent solutions. Machine learning offers the ability to analyze vast amounts of data, identify patterns, and improve decision-making processes in real-time, facilitating the development of more efficient and resilient control systems.
Furthermore, machine learning techniques such as reinforcement learning are enabling systems to learn from their environments and optimize their performance over time. This adaptive learning capability is particularly beneficial in environments with unpredictable variables or where system dynamics can change. By leveraging these advanced algorithms, engineers can design control systems that not only react to disturbances but also proactively adapt their strategies to enhance performance and reliability. As the integration of machine learning in control theory continues to evolve, it is setting the stage for the next generation of intelligent systems that can perform in ways previously thought unattainable.
